本文我们来简单聊一聊递归的问题,首先我们们先了解一下,什么是递归。在数学与计算机科学中,递归是指在函数的定义中使用函数自身的方法。实际上,递归,顾名思义,其包含了两个意思:递 和 归,这正是递归思想的精华所在。那么一个完整的递归应该具备哪些特点或者说是解题步骤呢?我认为应该有两点:
- 原问题可以生成若干个小问题,且所有问题的解决方式完全相同。
- 有一个结束条件。
那么,我们来简单的举一些例子:
第一题:阶乘问题
这是一道递归经典问题,阶乘 n!即n (n-1)(n-2)…… * 2 * 1,唯一特殊的是0 ,国际规定,0 的阶乘是 1。按照我们的递归思路,先观察递归时的解决方式是什么,n!是不是可以看作是n*(n-1)!,那么以此类推,是不是就可以一直推到结束,那么解决方式找到了,我们来寻找结束条件,那么通过我们对数学的了解,一般都是乘到 1 结束,1 的阶乘是 1 ,0 的阶乘也是 1 ,那么代码我们是不是可以这样写:
def factorial(n):
if n <= 1: # 当n小于等于1时返回1
return 1
else:
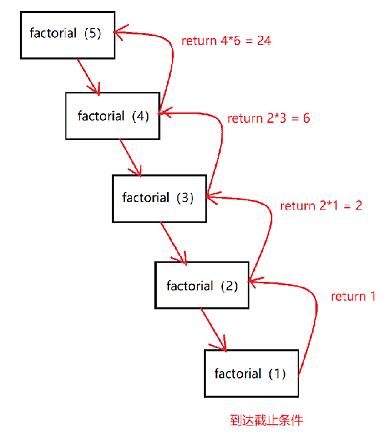
return n * factorial(n - 1) # 当n大于1时返回 n*(n-1)!那么这就是整个阶乘的代码部分,那么到底底层是如何实现的呢》给大家进行一个模拟。
** **
**
如图一所示,我们以factorial(5)为例,所谓递归,有递,有归。那么在图中我们可以看到,数据先向下进行传递,当触碰到底部的截止条件时,开始回溯(回归),那么从factorial(1)开始,一直返回到我们的结果。
那么在这个问题中我们大致了解了递归的基本原理,那么我们来看下一题进行一下巩固。
第二题:斐波那契数列
这也是一道递归的经典问题,还是按照我们的方式,先看解决方式,所谓斐波那契数列,就是后一项等于前两项的和,即f(n) = f(n-1)+ f(n-2),那么接下来我们考虑结束条件,我们知道,一般来讲,我们从第三个数开始算,因为第0个数和第一个数我们无法向下取两个,同时,第0个数和第一个数我们分别取0和1,那么按照这个思路即可找到截止条件为n <= 1。
**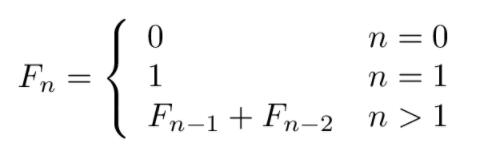 **
**
实现代码如下:
def fabonacci(n):
if n <= 1 : # 结束条件
return n
else:
return fabonacci(n - 1) + fabonacci(n - 2)这就是最基本的斐波那契数列的实现方式。那么我们来看一下这个实现过程是不是存在一些弊端。首先我们模拟一下过程,以fabonacci(5)为例:
fabonacci(5)= fabonacci(4)+ fabonacci(3)
fabonacci(4)= fabonacci(3)+ fabonacci(2)
fabonacci(3)= fabonacci(2)+ fabonacci(1)
fabonacci(2)= fabonacci(1)+ fabonacci(0)
fabonacci(1)= 1
fabonacci(0)= 0
那么我们可以看到,当我计算fabonacci(5)的时候,我需要知道 fabonacci(4)和fabonacci(3)的值,然后我们计算fabonacci(4)的时候还是需要知道fabonacci(3)的值,也就是说fabonacci(3)的值仅仅在这几次递归中就被运算了两遍,那么fabonacci(2)的值及fabonacci(1)的值都运算了数次,大大降低了效率。那么这个时候,我们可以考虑另一种递归算法,这个时候,我们考虑每次存入的数据均是本位的值带上其运算时n - 1位的值,这样的话我们可以减少运算次数,因为我们每一次的值都会由上一次的值直接进行加减,举一个例子,譬如说当n = 2时,我们就可以记fabonacci(2)的值为(1,1),第一位的1是该位置的值,而后一个的1是n-1位置,也就是1位置的1,那么这个时候,比如说我们想计算 n = 3时的值,是不是就可以 n = 2时的(1,1)进行1 + 1操作得到此时n = 3 位置的值(2,1),以此类推。实现代码如下:
def good_fabonacci(n):
if n <= 1:
return (n, 0)
else:
(a, b) = good_fabonacci(n - 1)
return (a + b, a)这个问题的实现就大大提高效率,将时间复杂度提高到O(n),那么是不是感觉这个方式有点像迭代的方式,其实原理类似,在这里就不给大家展示迭代的方式了,一层循环,很简单。
第三题:递归重写二分查找
在之前的文章中,我们学习了二分查找,不太理解的读者可以看一下之前的文章,那么我们想一下,是否可以用递归的方式实现呢?其实原理时一样的,只不过是将迭代方法转变成了递归方法,终止条件都是相同的,代码如下,相信大家在熟悉迭代法的二分后一眼就能看懂这个方式:
def binary_search_recursive(lis, val, left, right):
if left > right:
return False
else:
mid = (left + right) // 2
if val == lis[mid]:
return mid
else:
if val < lis[mid]:
return binary_search_recursive(lis, val, left, mid - 1)
else:
return binary_search_recursive(lis, val, mid + 1, right)问题四:全排列问题
什么是全排列,譬如说给两个字符 a,b那么全排列为[(a,b),(b,a)],三个字符a,b,c 排列方式为
[(a,b,c),(a,c,b),(b,a,c),(b,c,a),(c,a,b),(c,b,a)],那么大家是不是就理解了全排列的方式了?
那么我们如何实现它,也就是我们的步骤一,寻找解决方式,其实全排列是一个数字之间两两交换的过程,代码如下:
def allrange(lis, start, end):
if start == end:
for i in lis:
print(i, end=" ")
print()
for m in range(start, end + 1):
lis[m], lis[start] = lis[start], lis[m]
allrange(lis, start + 1, end)
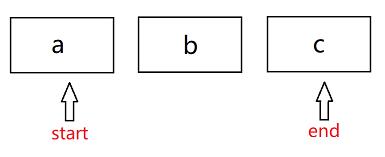
lis[m], lis[start] = lis[start], lis[m]给大家模拟一下三个字符的,大家可能就理解了。首先假设我有三个字符a,b,c,放在一个大列表lis中:
** **
**
那么,我们该如何移动呢,首先我们来找一个字符m当作我的交换位置,m从当前start位置开始到end位置截止,假设我们lis[m]先与lis[start]交换,其实a的位置不变,然后我们start + 1进行递归下一位b,m也改变,依旧是当前start位置的b,然后lis[m]与lis[start]交换,其实b也没变,然后再递归下一位,start + 1,我们结束条件是递归到start = end,此时我们可以输出了,那么这个时候输出的是 a,b,c,那么接下来我们进行回溯回溯到b。
** **
**
我们可以看到,m指针向后移动一位到了end位置,这个时候执行lis[m]与lis[start]交换,是不是就将原a,b,c转换为了a,c,b。
**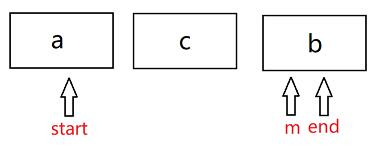 **
**
这就找到了所有a开头的排列方式,在结束之前,要lis[m]与lis[start]再交换,将数据归还成原样。如果大家还不是很懂,欢迎联系我,我为大家模拟一下四个字符的。
好了,以上就是递归的基本原理及部分经典习题解读,如果大家有哪里不理解可在评论区留言。