本期我们聊一聊二叉树的遍历。
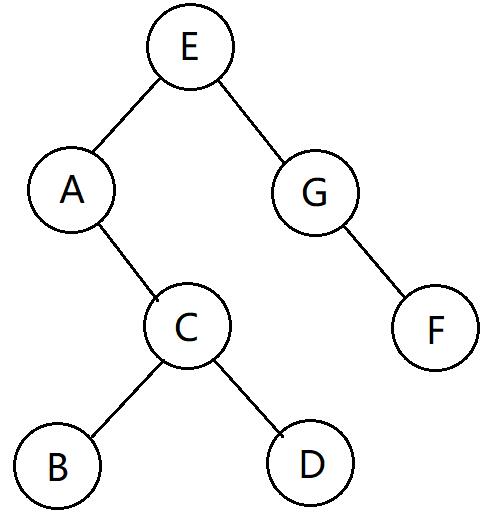
在讲堆排序的时候,已经为大家讲解了树的基本知识,不了解的同学可以去看一下堆排序的文章,在这里就不再赘述了。那么首先先画一棵简单的二叉树:
** **
**
然后我们用代码实现这棵二叉树:
class BitreeNode:
def __init__(self, data):
self.data = data
self.lchild = None
self.rchild = None
a = BitreeNode("A")
b = BitreeNode("B")
c = BitreeNode("C")
d = BitreeNode("D")
e = BitreeNode("E")
f = BitreeNode("F")
g = BitreeNode("G")
e.lchild = a
e.rchild = g
a.rchild = c
c.lchild = b
c.rchild = d
g.rchild = f那么,首先先给大家三种遍历的结果,大家根据遍历的结果,看看是否能推断出是如何进行遍历的。
前序遍历:E A C B D G F
中序遍历:A B C D E G F
后序遍历:B D C A F G E
其实大家根据结果与遍历名称其实也可以大致推断出遍历方式,我们假设有一个列表存取每次的结果,首先我们先来看前序遍历:所谓前序遍历,就是从根节点处开始,先找左子节点后找右子节点并不断递归的过程,以本文样例为例,从E开始,E进列表,找到左子节点A,A进列表,然后找A的左子节点发现没有,然后找A的右子节点C,C进列表,然后找C的左子节点B,找B的左子节点发现没有,找B的右子节点也没有,返回C,找到C的右子节点D,D进列表,D同B一样没有左右子节点,返回C,C均找过返回A,A返回E,找E的右子节点G,G进列表,找G左子节点没有找右子节点F,F进列表,找F没有左右子节点返回G,G返回E 结束。
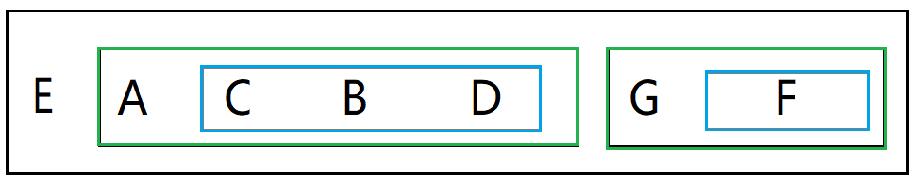
整个过程的图示为:
** **
**
从图示中我们可以看到,先将根节点放在队首,然后向后的两个空间存放左右两个新子树,然后新的子树再将根节点放在第一位,以此类推。我们来看一下代码实现:
def prev_order(root):
if root:
print(root.data, end=" ")
prev_order(root.lchild)
prev_order(root.rchild)接下来是中序遍历,所谓中序遍历,就是先遍历左子树再遍历根节点最后遍历右子树,以图为例,先遍历E的左子树(A C B D),然后找到根节点 A 遍历其左右子树,没有左子树,返回A,A进列表,遍历右子树(C B D),找到其根节点C遍历左子树B,B没有左子树,返回B,B进列表,B也没有右子树,返回C,C进列表,遍历C的右子树D,D没有左子树,返回D,D进列表,也没有右子树,证明左子树遍历结束,返回E,E进列表,然后遍历E的右子树,方法同上,先返回G,再返回F。
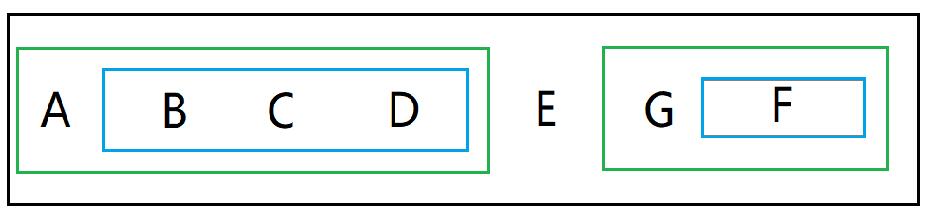
整个过程的图示为:
** **
**
由图示我们可以看到,先将根节点放于中间,左右两边各开辟一个空间分别存放左右子树,然后左子树内将新根节点放于中间,左右各开辟新空间存放新的左右子树,右子树同理。代码实现如下:
def mid_order(root):
if root:
mid_order(root.lchild)
print(root.data, end=" ")
mid_order(root.rchild)最后是后序遍历,所谓后续遍历,大家已经可以根据刚刚两个所讲的遍历方式推断出是如何遍历的了,就是先遍历左子树,再遍历右子树,最后回到根节点,以图为例,我们已知E是根节点,先观察左子树(A C B D),然后找到新根节点A,找其左子树发现没有,然后找其右子树(C B D),然后找到新根节点C,找其左子树B,发现没有左右子树后,返回B,B进列表,然后找C的右子树D,没有左右子树,返回D,D进列表,返回C,C进列表,然后返回A,A进列表,以A为根节点的左子树遍历完成,用同样的方法遍历E的右子树(G F),最后返回E。
整个过程图示为:
**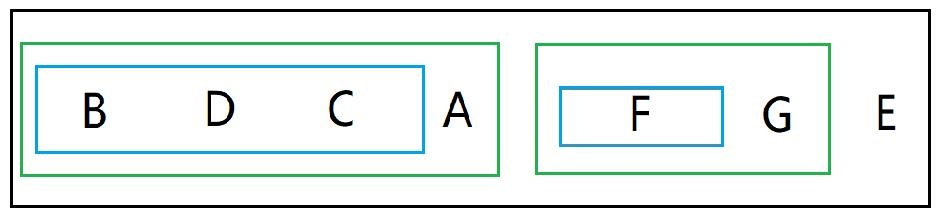 **
**
由图示我们可以看到,先将根节点放于尾部,然后前面开辟一前一后两个空间分别存放左子树右子树,然后方法同样,递归实现:
def post_order(root):
if root:
post_order(root.lchild)
post_order(root.rchild)
print(root.data, end=" ")最后,跟大家聊一聊根据遍历结果复原树的方法,这个时候,我们需要以下两种条件:
- 前序遍历 + 中序遍历
- 中序遍历 + 后序遍历
注意,这两个条件中我们都看到了中序遍历,中序充当了胶水的重要角色,那么如何实现呢,给大家模拟一下,
首先,我们观察到前序遍历的第一个字母E,证明整个树的根节点是E,然后我们观察中序遍历,找到E,那么E的两端就分别是其左子树(A B C D)和右子树(G F)了。这个时候,我们就可以把E画在纸上了,然后看前序遍历,找到左子树的四个元素,A是第一个,证明A是此左子树的根节点,然后再回到中序遍历找这个左子树,发现A左面是没有元素的,证明A是没有左子树的,同时A的右子树就是(B C D),然后再先到前序遍历中找到C,然后回到中序遍历中找到C的左右两端,以此类推,我们是不是就能画出E的左子树:
** **
**
那么按照同样的方式,是不是就可以也可以画出E的右子树。
那么中序遍历 + 后续遍历的寻找方式是不是也是一样的呢?大家自己做一做,有不会的地方,欢迎在评论区里留言。