上期文章中,我们通过迷宫问题引入了深度优先搜索,采用了一种利用栈的思想,在本文中,将为大家引入广度优先搜索的思想,利用了一种队列的方式。首先,什么是广度优先搜索?广度优先搜索算法(Breadth-First Search,BFS)是一种盲目搜寻法,目的是系统地展开并检查图中的所有节点,以找寻结果。换句话说,它并不考虑结果的可能位置,彻底地搜索整张图,直到找到结果为止。BFS并不使用经验法则算法。
那么,广搜与深搜的区别是什么呢?其实很容易区分,深搜可以理解为按照顺序来搜索,譬如说我能走上就绝不走下了,直到没路了再回溯回来尝试向下走,而广搜不同,广搜同时走很多路径,只要能走,就全都一起走,直到有一个点到了终点就终止搜索,接下来,给大家模拟一下使用广度优先搜索的过程,就一目了然了。
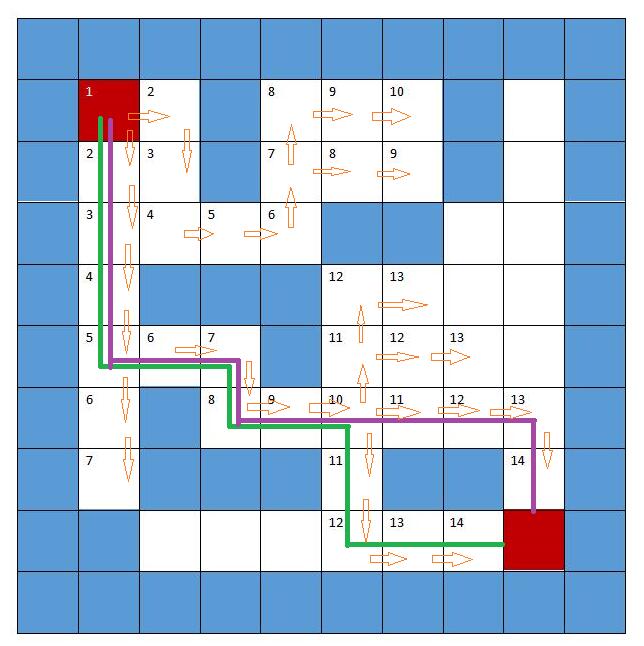
我们依旧以之前的图说明,先声明一下,图中的数字是走的第几次,也就是到第几步,箭头是说明该点是哪个节点的下一节点,说白了就是两个点之间的引出关系,方便大家的理解。
** **
**
由图我们可以看出,一个节点可以同时引出不止一个节点,直到最终有点触碰到了终点,则停止继续搜索,其实可以看出,广搜搜索到的路径一定是最短路径。
接下来给大家聊一下广搜路径的输出方式,在上文中我们已经了解到,每一个节点都是被其上一节点所引出,找到终点后,其实我们需要对路径进行回推。因此,每一个节点,我们都需要有一个下标作为其地址,方便最后的反向找路。那么就会有人提出问题,如何获得下标,规则是什么?我们假定一个列表(path),用于存取这些坐标,那么我们可以考虑以元组形式进行存储即(横坐标,纵坐标,下标),那么当第一个元素进队后,将其出队存储于我们新创建的path列表中,然后寻找下一个节点,那么下标如何定义,我们举一个简单的例子:
** **
**
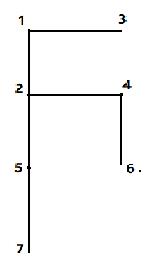
如上图,我们想从 1 走到 7。
首先是1 进队列,然后存入path列表中,由于它是首元素,我们给它个下标 -1,我们观察到下一次进队的可以有2和3,那么2和3的下标该怎么给,可以采取这个规则,看是谁让它来的,比如说2和3,是1让他俩来的,那么给他俩的下标就都是 1 的位置 0 ,再往下看,4和5都是由2引进来的,那么他俩的下标就是2这个元素的位置 1,接下来就是7由5引进,7下标是5的位置,以此类推。
那么我按照广搜加下标是不是可列出下面的表格:
** **
**
接下来,我们就可以按这个表格,从7往回找,7按下标找到5,5找到2,2找到1,发现1的下标是-1 则终止。
那么如何思路有了,如何进行代码实现呢?首先我们可以调用队列的类库:
from collections import deque然后我们依然用上次的迷宫以及四种移动方式:
maze = [
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
[1, 0, 0, 1, 0, 0, 0, 1, 0, 1],
[1, 0, 0, 1, 0, 0, 0, 1, 0, 1],
[1, 0, 0, 0, 0, 1, 1, 0, 0, 1],
[1, 0, 1, 1, 1, 0, 0, 0, 0, 1],
[1, 0, 0, 0, 1, 0, 1, 0, 0, 1],
[1, 0, 1, 0, 0, 0, 1, 0, 0, 1],
[1, 0, 1, 1, 1, 0, 1, 1, 0, 1],
[1, 1, 0, 0, 0, 0, 0, 0, 0, 1],
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
]
dircs = [
lambda x, y: (x + 1, y),
lambda x, y: (x - 1, y),
lambda x, y: (x, y + 1),
lambda x, y: (x, y - 1),
]接下来就是主题代码了,首先我们先模拟出输出函数:
def print_path(path):
headnode = path[-1] # 首先找到存的最后一个位置
real_path = [] # 定义一个新列表存放坐标
while headnode[2] != -1: # 只要下标不为 -1
real_path.append(headnode[0:2]) # 将该坐标放入新列表
headnode = path[headnode[2]] # 新判断位置
real_path.append(headnode[0:2]) # 将起点放入
real_path.reverse() # 倒叙输出
for node in real_path:
print(node)最后就是广搜的部分了:
def maze_path_queue(x1, y1, x2, y2):
queue = deque() # 定义一个队列
maze[x1][y1] = 2 # 标记起点走过
queue.append((x1, y1, -1)) # 将起点放入队首
path = [] # 定义路径列表
while len(queue) > 0: # 只要队列不为空
headnode = queue.popleft() # 队首出列
path.append(headnode) # 将队首放入路径内
if headnode[0] == x2 and headnode[1] == y2: # 如果发现此时队首是终点则输出
print_path(path)
return True
for dir in dircs: # 执行移动方法
nextnode = dir(headnode[0], headnode[1])
if maze[nextnode[0]][nextnode[1]] == 0: # 如果下一个点是可走点
queue.append((nextnode[0], nextnode[1], len(path) - 1)) # 下一节点入队并记录下标
# 下标记录谁带它来的
maze[nextnode[0]][nextnode[1]] = 2 # 标记该点已经走过
else:
print("There is no way!") # 如果队空,则证明没有路
return False这就是整个迷宫问题的解决方式,大家有哪些不懂的地方可发布在评论区。