在数据结构中,我们先学习的是栈和队列,在本文中,我们来简单聊一聊栈。栈(stack)又名堆栈,它是一种运算受限的线性表。限定仅在表尾进行插入和删除操作的线性表。这一端被称为栈顶,相对地,把另一端称为栈底。向一个栈插入新元素又称作进栈、入栈或压栈,它是把新元素放到栈顶元素的上面,使之成为新的栈顶元素;从一个栈删除元素又称作出栈或退栈,它是把栈顶元素删除掉,使其相邻的元素成为新的栈顶元素。
** **
**
由上图我们可以看出,栈的底部是封死的,因此栈的特点就是先进后出,后进先出。
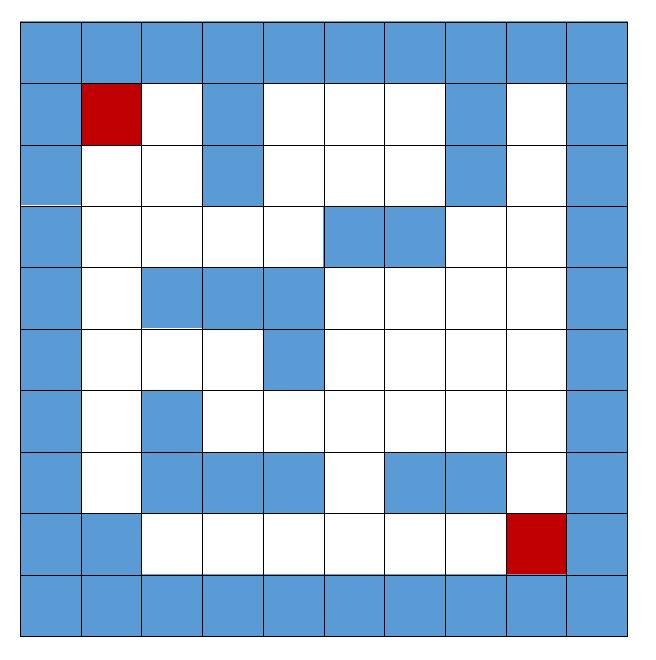
现在我们来看一道迷宫问题,现在想从上边的红块走到下面的红块,期间,我们需要避开所有的蓝块,且只可以选择 上、下、左、右四个方向来移动,最终请输出每次移动的坐标,若不存在这条道路,就输出没有该路径。
** **
**
可见上图,为本次的迷宫示意图,为方便大家代码实现,现给出该迷宫的数字表达形式:
maze = [
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
[1, 0, 0, 1, 0, 0, 0, 1, 0, 1],
[1, 0, 0, 1, 0, 0, 0, 1, 0, 1],
[1, 0, 0, 0, 0, 1, 1, 0, 0, 1],
[1, 0, 1, 1, 1, 0, 0, 0, 0, 1],
[1, 0, 0, 0, 1, 0, 1, 0, 0, 1],
[1, 0, 1, 0, 0, 0, 1, 0, 0, 1],
[1, 0, 1, 1, 1, 0, 1, 1, 0, 1],
[1, 1, 0, 0, 0, 0, 0, 0, 0, 1],
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
]其中,1 代表不可走的蓝块,0 为可走的白块,(1,1)为起始点,(8,8)为终止点。
那么这道题该如何解决呢?
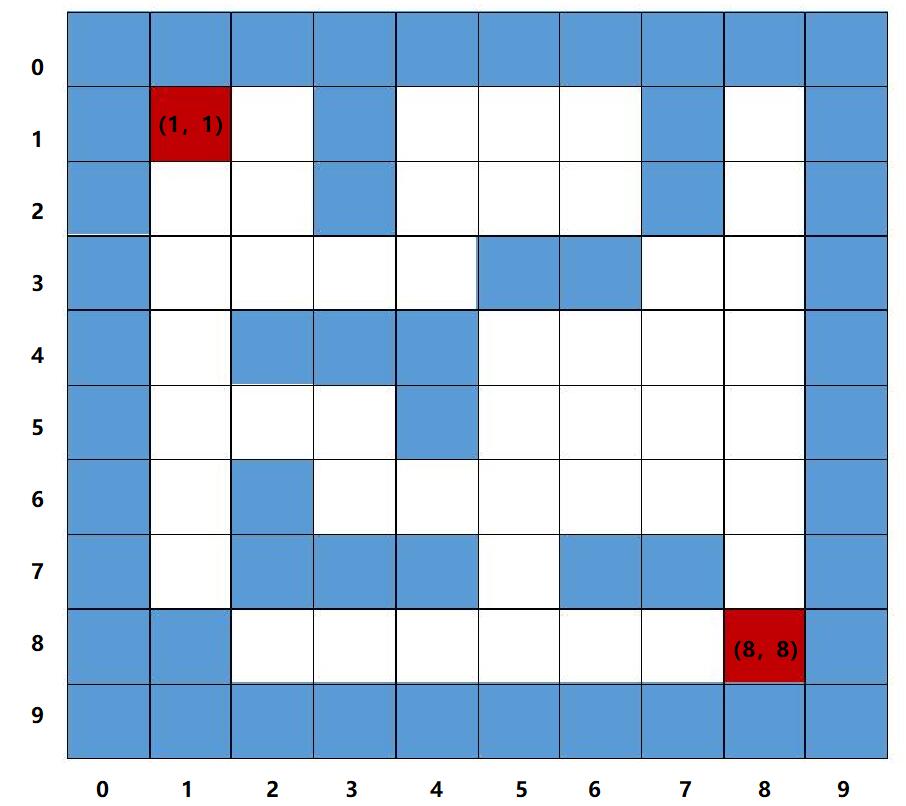
首先给大家引入一下深度优先搜索的思想:深度优先搜索属于图算法的一种,是一个针对图和树的遍历算法,英文缩写为DFS即Depth First Search。那么以本题为例,先为大家模拟一下深度优先搜索的过程,以帮助以后更好的理解深度优先搜索。我们首先为这个迷宫设定好坐标:
** **
**
由上图,我们已经坐标化整个迷宫,现在已知我们只有上、下、左、右这四种移动方式,假定我们按照上下左右的顺序选择了一种方式且可以移动(即下一个块不是蓝块)就不执行其他移动方式(即如果发现上可走,就不要考虑其他移动方式了,上不行就换右)。同时,走过的块我们要将其标记为蓝块,或是其他颜色的块,以区分未走过的白块。现在请根据我以下所写的坐标来看每一步所走的路径:
(1,1)->(2,1)->(2,2)->(2,3)->(3,3)->(4,3)->(4,2)->(4,1)->(5,1)
->(6,1)->(6,2)->(5,2)->(4,2)。
注意,在这个时候我们会发现(4,2)这个点我们之前走过了,那么这个时候,这个点我们就不能再走了,也说明了,这条路径就是不通的,那么怎么办,我们返回上一个点(6,2),去观察他还有没有路能走,只要下一步不是白块,就可以走,因此,我们以此类推,最终退到(2,3)这个点继续模拟:
(2,3)->(1,3)->(1,2)发现五路可走,那么回退至(1,3)发现可向下走,于是(1,4)->(1,5)以此类推,直到最终观察能否到达(8,8)。
这既是整个过程的一个思路,也是深搜的基本思想,大家可以从整个过程中看出,是不是这个方式运用的是栈的原理,我们永远取的是栈的栈顶元素进行查找,可以就留在栈内,不可以就出栈,查看新一个栈顶元素,下面我们来代码实现一下:
首先我们先定义四个移动方式,这里可以使用lambda表达式:
dircs = [
lambda x, y: (x + 1, y),
lambda x, y: (x - 1, y),
lambda x, y: (x, y + 1),
lambda x, y: (x, y - 1),
]接下来就是搜索的过程:
def maze_path(x1, y1, x2, y2):
stack = []
stack.append((x1, y1)) # 列表中传入的是坐标
while (len(stack) > 0): # 只要栈不为空
topnode = stack[-1] # 当前的栈顶元素
if topnode[0] == x2 and topnode[1] == y2: # 当检测到该点就是终点时输出栈内所有元组
for i in stack:
print(i)
return True
for dir in dircs: # 从四种方向中选取走向
nextnode = dir(topnode[0], topnode[1]) # 查找下一个点的坐标
if maze[nextnode[0]][nextnode[1]] == 0: # 如果该点是白块
stack.append(nextnode) # 这个点入栈
maze[nextnode[0]][nextnode[1]] = 2 # 将该点赋值为2 证明该点已经走过
break
else:
stack.pop() # 如果没有下一个点,则进行出栈操作
else:
print("There is no way!") #栈空则证明没有路
return False这就是一个简单的深搜过程,其实在这个过程中我们只需要注意,走过的点一定要进行标记即可。