这次要和大家聊一聊归并排序,那么什么是归并排序呢,首先给大家举一个简单的例子:
** **
**
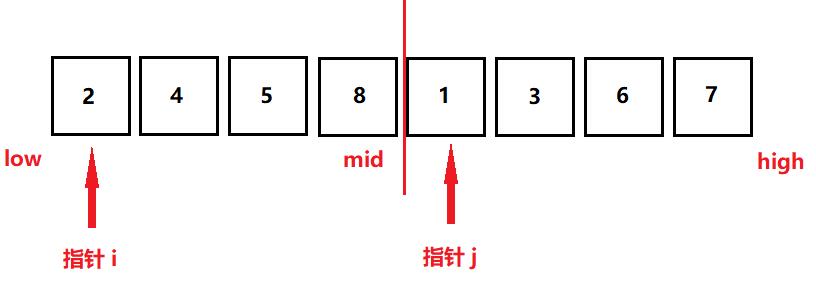
如上图,我们得到一个列表,其实这个列表有一个规律,那就是如果我们从中间截断,左右两边的小列表其实是有序的,在学习数据结构时,我们学习过一个经典例题,合并两个有序数组,那么这个时候是不是可以像合并数组那样合并这两个有序数列。
** **
**
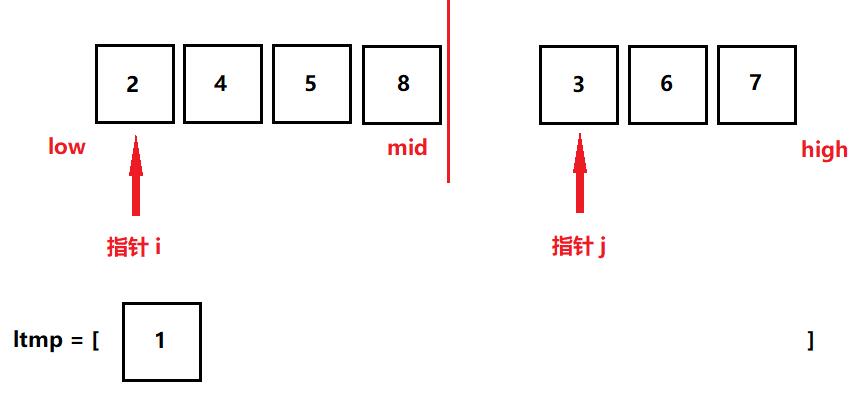
如上图,我们把这个列表分为两段,标记好起始元素位置(low)和终止元素位置(high)以及两地址的中间地址(mid),其实,我们已经把整个列表以mid为中心,分成两个小列表了,这个时候就可以利用归并(merge)的思想,首先我们取到两个指针,i,j,这两个指针分别指向两个小列表的第一个元素,这个时候,我们比较i位置的元素大小和j位置的元素大小,我们假设这个列表为lis,那么lis[i] < lis[j]的话,是不是就可以断定,lis[i]此时的元素就是最小的元素了,反之,要是lis[j] < lis[i],那么lis[j]就是整个列表中最小的元素,这个时候我们就可以把这个最小的元素取出放于一个新列表的首位,我们假设这个新列表是ltmp,这个时候,按照我们的例子,1 就被取下放置于我们的新列表中了,同时,j指针的位置要向后移动一位。
** **
**
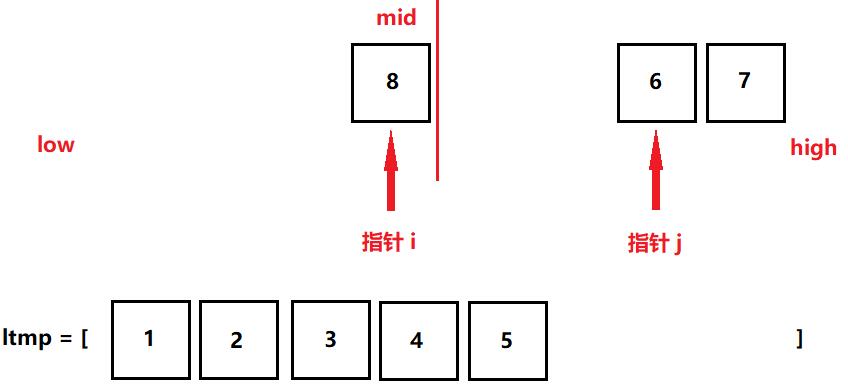
以此类推,比较i位置与j位置的大小关系,然后把每一次的最小值暂存到新列表(ltmp)中,不要忘记指针随着原位置数的取出而后移。
** **
**
那么什么时候终止呢?有两种情况,第一种是 i 指针大于mid位置的时候,第二种是 j 指针大于high位置的时候。终止后会也会发现两种情况,要么是左边的小列表数字有剩余,要么是右边的小列表数字有剩余,这个时候,我们知道,左右两边的列表其实是有序的,那么本身不需要再进行排列了,直接放到新列表(ltmp)的末尾就好,最后,我们只要把新列表(ltmp)再归还给原列表(lis)就完成了一次归并(merge)。代码如下:
def merge(lis,low,mid,high):
i = low
j = mid + 1
ltmp = []
while i <= mid and j <= high:
if lis[i] < lis[j]:
ltmp.append(lis[i])
i = i + 1
if lis[j] < lis[i]:
ltmp.append(lis[j])
j = j + 1
while i <= mid:
ltmp.append(lis[i])
i = i + 1
while j <= high:
ltmp.append(lis[j])
j = j + 1
lis[low:high+1] = ltmp接下来就是整个归并排序的核心了,在实际排序过程中,我们几乎很少能遇到上文这种理想的情况,我们得到的列表大多是无序的。那么,如何能通过归并的方式得到排序的结果呢?
** **
**
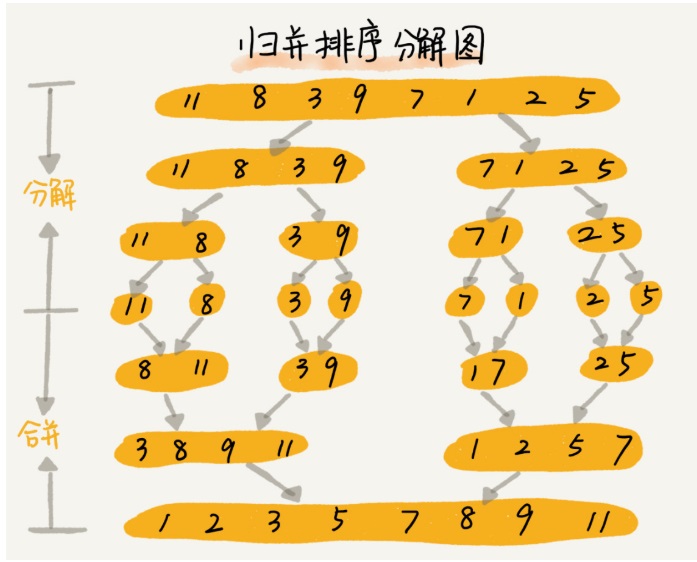
答案是采取一种递归的思想,先分解再合并,我们将原列表分解为一个个的小列表,每个小列表之间进行归并(merge),然后最终小列表合并成大列表,如下图所示,即可得到一个有序列表。
归并排序代码如下:
def merge_sort(lis,low,high):
if low < high:
mid = (low + high) // 2
merge_sort(lis,low,mid)
merge_sort(lis,mid+1,high)
merge(lis,low,mid,high)
return lis是不是看起来很简单,但是理解起来有些难度,这里采用递归的思想,假如,代码的倒数第二行我们不进行归并,而是对此时的递归进行打印:
def merge_sort_view(lis,low,high):
if low < high:
mid = (low + high) // 2
merge_sort_view(lis,low,mid)
merge_sort_view(lis,mid+1,high)
print(lis[low:high+1])那么我们会得到如下的结果:
[11, 8]
[3, 9]
[11, 8, 3, 9]
[7, 1]
[2, 5]
[7, 1, 2, 5]
[11, 8, 3, 9, 7, 1, 2, 5]
可以看出,我们在递归过程中,只有当low和high均为 1 时会结束递归,然后当加上归并(merge)函数后,即可进行合并。
归并排序的时间复杂度无论什么情况都是O (nlogn),归并排序是Python内置sort函数的底层之一,内置函数是基于归并排序和插入排序的优化算法,因此,学习Python,了解归并排序是必不可少的。