学习过堆排序后,今天我们来学习一下堆排序,在学习堆排序之前,我们首先来简单学习一下树的基本知识。
树是一种数据结构,它是由n(n>=1)个有限结点组成一个具有层次关系的集合。虽然将其称之为树,但它是树根在上,叶子在下的结构,每棵树都具有如下特点:
- 每个结点有零个或多个子结点
- 没有父结点的结点称为根结点
- 每一个非根结点有且只有一个父结点
- 除了根结点外,每个子结点可以分为多个不相交的子树

现在我们已经大致了解了树的基本形状了,那么在树这个大类中,有着一个特殊的分类—-二叉树,二叉树是n个有限元素的集合,该集合或者为空、或者由一个称为根(root)的元素及两个不相交的、被分别称为左子树和右子树的二叉树组成,是有序树。当集合为空时,称该二叉树为空二叉树。在二叉树中,一个元素也称作一个结点。
**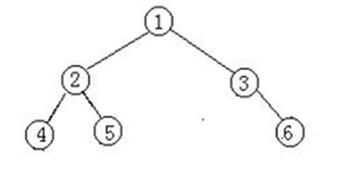 **
**
在二叉树中,有一个更加特殊的分支—-完全二叉树
一棵深度为k的有n个结点的二叉树,对树中的结点按从上至下、从左到右的顺序进行编号,如果编号为i(1≤i≤n)的结点与满二叉树中编号为i的结点在二叉树中的位置相同,则这棵二叉树称为完全二叉树。
**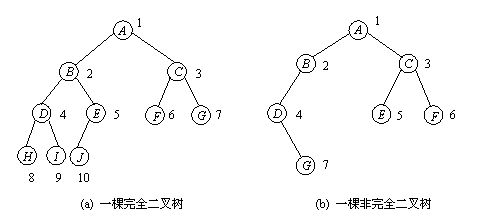 **
**
我们看上图的这个完全二叉树,如果我们将其位置编号如下,会不会发现如下的规律:
左子节点 = 2 * 父节点 + 1
右子节点 = 2 * 父节点 + 2
同理,当我们知道子节点编号是时,同样可以通过 (子节点 - 1)// 2 来得到父节点的位置。
现在我们已经大致了解了从树到完全二叉树的一个变换,下面我们来学习一种筛选算法(sift)
所谓筛选,就是将已有的二叉树进行重新排列,进而得到大根堆的一个过程。
**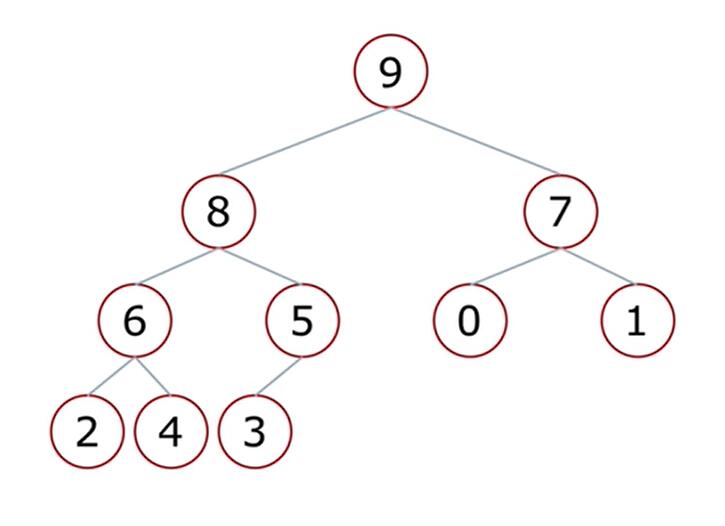 **
**
由上图我们可以看出,大根堆是每一个父节点都会大于子节点的值。所以,简单来说,筛选的方式就是让每一个父节点的子节点都小于它就好。那么具体筛选方式是什么样的呢,现在一起来模拟一下:
首先先给到一个完全二叉树:
**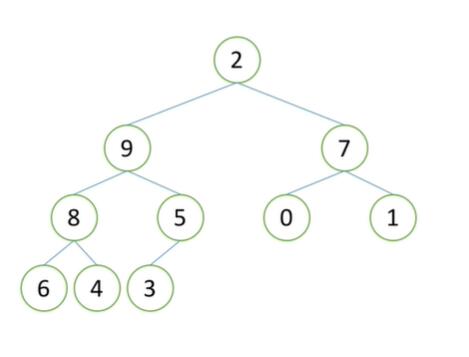 **
**
如上图,我们观察根节点位置是 2 ,那么按照我们的原则,父节点应比其子节点大,因此这个 2 不配在根节点位置,这个时候,我们把 2 拿出二叉树,将其位置空出。
**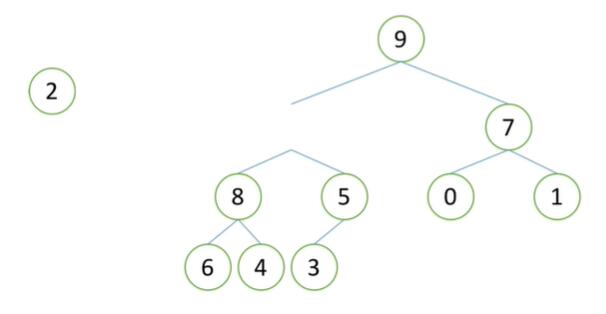 **
**
可以看到,现在根节点的位置是空缺的,此时,我们应找到一个数字对根节点进行补全,观察其左右两子节点,发现 9 > 7 ,因此将 9 置于根节点位置,现在, 9 的位置空出,此时,我们考虑是否将 2 放进去,观察原 9 位置的两个子节点 8 与 5 ,均比 2 要大,因此不能将 2 插入,比较两子节点,可发现 8 > 5 ,因此将 8 填入空缺位置,然后 8 的位置空缺,以此类推,6 补空位,最终将 2 置于原 6 的位置即可完成本次筛选 ,最终,对于每一个节点进行sift函数之后即可得到一个大根堆。
** **
**
其实现代码如下:
def sift(lis,root,last): #root为根节点 last为最后一个元素位置
i = root
j = 2 * i + 1 #j是左孩子
tmp = lis[root] #储存堆顶
while j <= last: #确定终止循环条件
if j + 1 <= last and lis[j+1] > lis[j]: #比较左右两子节点
j = j + 1
if lis[j] > tmp:
lis[i] = lis[j]
i = j #将指针指向空位置(父节点)
j = 2 * i + 1
else:
lis[i] = tmp #如果小于,则root归位
break
else:
lis[i] = tmp #循环结束后,root归位可以看出,无论是否完成,最终都要进行root值的归位,那么,其实我们是不是可以在代码当中直接进行简化呢?大家可以在评论区说出你的答案。
接下来就是实现堆排序的环节了,我们采取一种倒着取的原则。毋庸置疑,此时的最顶点的 9 是我们刚刚算法派出的最大值。 那现在直接将其取下,作为我们列表中的最大值。
**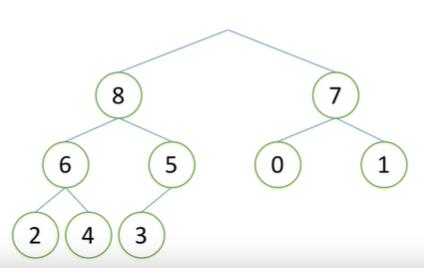 **
**
那么接下来该如何取,一定有很多人会想,那我用 8 去补位,实则不然,可以试想一下,8 补了 9 的位置接下来6 补 8,4 补6,可是就没有元素可以补4了,我们现在需要的是一颗完全二叉树。因此,我们这个时候选择最后一个元素 3 作为补位项,然后再通过一次sift算法,将 8 移至顶点,然后将 8 取走,以此类推,最终得到排序好的数列。
代码如下:
def heap_sort(lis):
n = len(lis)
for i in range((n-2)//2,-1,-1): #从最后一个节点的父节点开始,从右向左进行筛选
sift(lis,i,n-1)
for i in range(n-1,-1,-1):
lis[0],lis[i] = lis[i],lis[0] #将最后一个数与第一个数进行交换,重新筛选
sift(lis,0,i - 1)最终,即可取得排序好的列表,由代码可见,堆排序的时间复杂度为O (nlgn)。
其实,即使堆排序和快速排序的时间复杂度都是O (nlgn),但是在实际操作中,还是快速排序会快一些,堆排序也有它独有的优势,例如说我们要解决的TopK问题,例如说我想要找到某个数列中最大的前K个数,那么我们可以考虑以下几点,第一个是排序后切片,其时间复杂度为O (nlgn),第二种是利用基本排序方式,例如冒泡排序,其时间复杂度为O (Kn),如果K < lgn,那么其实第二种方法是快于第一种的,那么第三种方式就是利用堆排序的逐一出数,取前K项。其时间复杂度为O (nlgK),时间应为最低。但这种方式与堆排序不同,这需要将原二叉树变换为小根堆,在上文我们提及了大根堆,保证每一个父节点都大于其子节点,那么同理,小根堆中,所有父节点也一定小于子节点,代码如下:
def sift(lis,root,last):
i = root
j = 2 * i + 1 #j是左孩子
tmp = lis[root]
while j <= last:
if j + 1 <= last and lis[j+1] < lis[j]: #注意,这里的小根堆相较于大根堆改成了小于号
j = j + 1
if lis[j] < tmp: #同理,这里也要变为小于号
lis[i] = lis[j]
i = j
j = 2 * i + 1
else:
lis[i] = tmp
break
else:
lis[i] = tmp
def topk(lis,k): #选择前K项的函数
heap = lis[0:k]
# 1.建堆
for i in range((k-2)//2,-1,-1):
sift(heap,i,k-1)
#2.遍历
for i in range(k,len(lis)-1):
if lis[i] > heap[0]:
heap[0] = lis[i]
sift(heap,0,k-1)
#3.出数
return heap