快速排序

排序

发布日期: 2020-10-02

在排序算法中，有多种排序方式，例如比较低级的：冒泡排序、选择排序、插入排序。还有相对高级一些的排序方式，比如说这次要说的快速排序。快速排序相较于三种低级排序的优势在于其时间复杂度较小O (nlogn)，其利用了递归的思想，相较于循环结构，大大缩减了其排序时间，那么，快速排序的思想及原理是什么，下面我们来模拟一下。

图一

以上图为例，在介绍快速排序之前，首先想介绍一种算法，分割法（partition），这种算法实现的目的如下：

图二

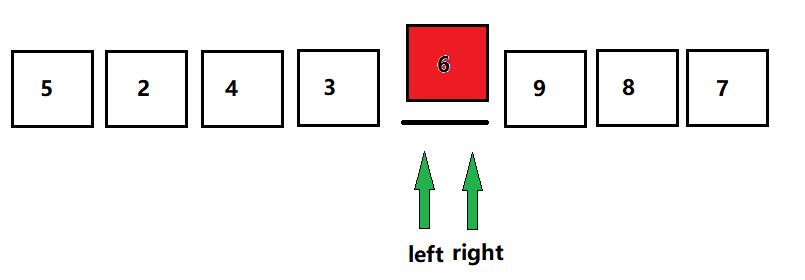
分割后的结果如下，可以看出，我们以首部数字作为基准，左侧的数字都比该数字要小，右侧的数字都比它要大，那么我们就可以用一种递归的思想进行排序了，例如说，基于上图，我们再对6的左右两边各进行一下partition函数，是不是就可以得到以下结果：

图三

以此类推，是不是就能得到我们想要排序顺序了，但注意，在本次示例中函数的调用出现了一个问题，后续会给大家解释。
说了这么多，那什么是分割法（partition），它的原理思想是什么，下面我们一起看一下：
所谓分割法，就是取列表中的一个数，其余的数以它为基准，小于基准数的放于左侧，大于基准数的放于右侧，可是放置的方法是什么？下面给大家模拟一下：
还是以图一的列表为例，首先我们取首部数字为基准数字，如图一所示，我们取 6 作为基准数字，接下来开始进行模拟，假设我们设有两个指针分别置于左右两端（left，right）：

图四

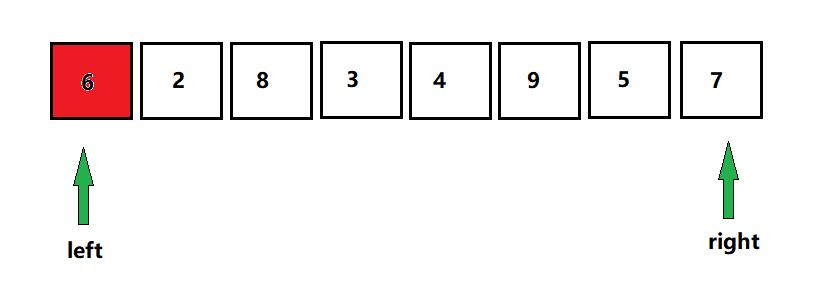
第一步，我们将首部的数字移开，那么该位置将变成一个空位置：

图5

那么这个时候，left指针指向为空，我们需要从right指针处开始寻找，寻找一个比基准值小的数将它置于现在left指针所指向的空位置。right指针处的数字与基准数进行比较，若小于基准数，则将它置于left指针处，若大于，则right指针进行左移，以此类推，以本文数据为例，从最右侧的 7 进行比较，大于基准数则左移，5 小于6，则 5 填补空缺位置：

图六

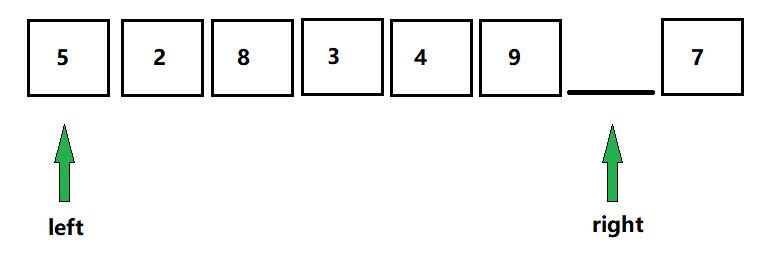
现在我们将五填补到了left指针所指的空缺位置，但此时我们会发现，right指针处出现了空缺，这个时候我们千万不要将基准数填补至空缺位置，而是采取和之前一样的办法，反过来，从left指针处开始，寻找比基准数要大的数来填补空缺，应从left指针处开始找，小于则left指针右移，大于则将该位置的数进行填补。由图六所示，从 5 开始，找到 8 ，然后将 8 填补到right指针所指位置，同时将left指针所指位置：

图7

以此类推，left指针空缺，再从right指针开始寻找比基准数小的数填补空缺，反之，right指针处空缺，从left指针处寻找比基准数大的数填补空缺。直到left指针与right指针相遇了，那么将基准数填入此时left指针所指位置，即完成了整个分割过程。

图8

由此，就是我们整个分割算法的实现过程了，接下来就是代码的实现了。代码如下：

  def partition(li,left,right):  #划分  
    tmp = li[left]               #设定tmp的值为基准值
    while left < right:  
        while left < right and li[right] >= tmp:  
            right = right - 1  
        li[left] = li[right]     #若判断发现小于基准数，则将其填补空缺 
        while left < right and li[left] <= tmp:  
            left = left + 1  
        li[right] = li[left]     #若判断发现大于基准数，则将其填补空缺 
    li[left] = tmp               #基准值归位 
    return left                  #返回右指针位置

接下来就是最终的代码实现了，快速排序是递归的过程，上文我们讲过，在基准数左右两边分别进行partition函数即可，首先基于partition函数的返回值，我们可以确定每一次基准数的最终位置，以此为中心，开始左右两边的递归，最终得到顺序结构。

    def _quick_sort(li, left, right):  
      if left < right:             
        mid = partition(li,left,right) #找到每一次的基准数位置  
        _quick_sort(li,left,mid - 1)   #左侧递归
        _quick_sort(li,mid+1,right)    #右侧递归
    def quick_sort(li):                 #简化快排函数的参数
        _quick_sort(li,0,len(li) - 1)

注意：